Il comportamento di un gas reale è approssimabile a quello di un gas ideale in certi intervalli di pressione e temperatura, mentre in altre condizioni può discostarsi anche in maniera significativa.
Le maggiori deviazioni dal comportamento ideale sono dovute a due fattori:
- Il volume occupato da una singola particella gassosa.
- La presenza di interazioni tra le particelle.
Il fattore di compressibilità
Per un gas ideale il rapporto PV/nRT = 1 per ogni valore di pressione e temperatura.
Per un gas reale si introduce una nuova grandezza chiamata fattore di compressibilità Z:
Tanto più il comportamento del gas reale si avvicina quello ideale, tanto più il valore di Z tende a 1.
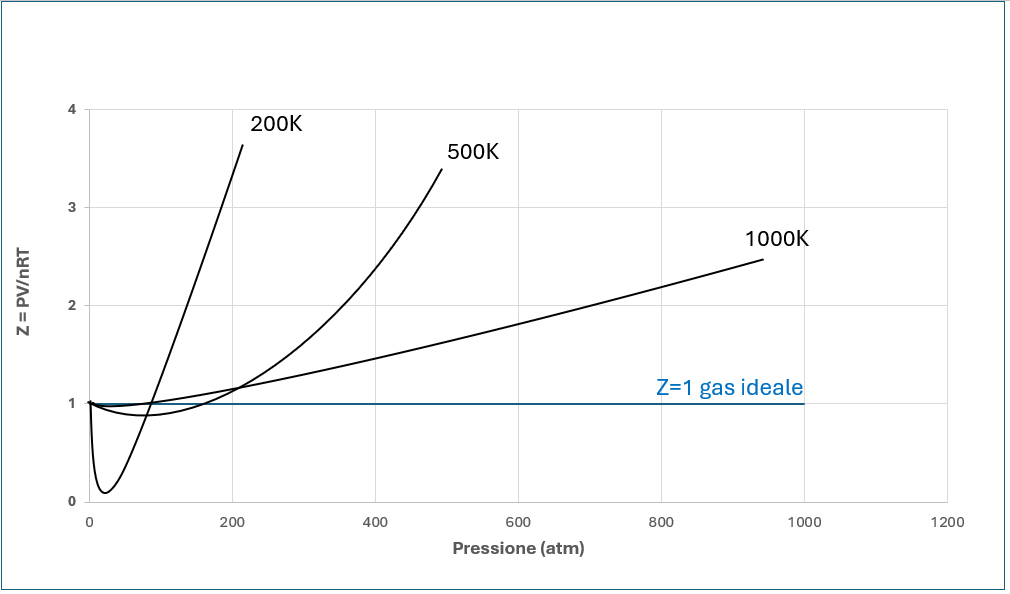
A valori più bassi di pressione, il valore di Z può scendere al di sotto di 1. Questo può essere spiegato considerando un gas reale più comprimibile di un gas ideale in virtù delle forze di attrazione tra le particelle che facilitano il loro avvicinamento.
A parità di pressione esercitata, il recipiente contenente un gas reale viene ridotto a un volume minore rispetto a quello contenente un gas ideale.
A più alti valori di pressione inizia a farsi sentire l’effetto del volume occupato dalle singole particelle che rende più difficoltosa la compressione. A parità di pressione esercitata, è questa volta il recipiente contenente il gas ideale a essere ridotto a un volume minore rispetto a quello contenente un gas reale.
Al crescere della temperatura vi è un incremento dell’energia cinetica posseduta dalle particelle le quali acquistano anche una maggiore mobilità. Questi effetti rendono meno consistente l’attrazione tra le particelle così come tendono ad aumentare la loro distanza vanificando l’effetto del volume proprio di ciascuna di essa. Aumentando la temperatura, il comportamento di un gas reale è approssimabile a quello di un gas ideale.
EQUAZIONE DI VAN DER WAALS
Johannes Van Der Waals propose una correzione all’equazione di stato dei gas ideali, tenendo conto dell’effetto del volume occupato da una singola particella e delle interazioni di natura attrattiva presenti.
L’equazione di Van Der Walls può essere scritta come:
CORREZIONE DEL VOLUME
Il termine volume può essere corretto tenendo conto che le particelle gassose non sono puntiformi ma occupano uno spazio (covolume) che non è accessibile a un’altra particella.
V = Videale – nb
- n = numero di moli di gas
- b = costante legata alle dimensioni delle particelle
CORREZIONE DELLA PRESSIONE
Quando una molecola urta contro la parete del recipiente, la forza d’impatto viene attenuata dall’attrazione esercitata delle altre particelle al centro. Questo effetto è tanto più marcato quanto maggiore è la densità di particelle nel recipiente e quanto maggiore è l’effetto intrinseco d’interazione.
Preale < Pideale
Nell’equazione di stato dei gas ideali occorre introdurre un termine correttivo che aggiunga alla pressione misurata un termine proporzionale al livello d’interazione tra le particelle e al quadrato della densità tra le particelle.
- n = numero di moli
- a = termine che tiene conto dell’effetto intrinseco delle interazioni tra le particelle
Le molecole che interagiscono tra loro più fortemente sono quelle che risentono maggiormente della deviazione dal comportamento ideale. Un esempio è rappresentato dall’ammoniaca le cui molecole interagiscono tra loro più fortemente rispetto alle molecole di idrogeno e azoto in virtù dei legami a idrogeno.

CONCETTI CHIAVE:
- I gas reali hanno un comportamento che si discosta da quello ideale.
- A più basse pressioni l’effetto delle attrazioni rende un gas reale più comprimibile di uno ideale.
- A più alte pressioni l’effetto del covolume rende un gas reale meno comprimibile di uno ideale.
- L’equazione di Van Der Waals corregge l’equazione di stato dei gas ideali tenendo conto di questi effetti.
