Categoria: Teoria

LEGGE DI HENRY

La legge di Henry governa gli equilibri liquido-gas. Secondo tale legge, a una data temperatura, un gas si scioglie in un liquido fino a che la pressione esercitata sulla superficie del liquido uguaglia la pressione che il gas esercita al suo interno.

In un sistema chiuso, raggiunta la condizione di equilibrio, il numero di molecole di gas che nell’unità di tempo passano dalla fase liquida alla fase gassosa uguaglia il numero di molecole che dalla fase gassosa passa alla fase liquida.

All’aumentare della pressione si ha una maggiore solubilità del gas nel liquido. L’equilibrio è pertanto caratterizzato da una maggiore quantità di gas disciolta nel liquido.

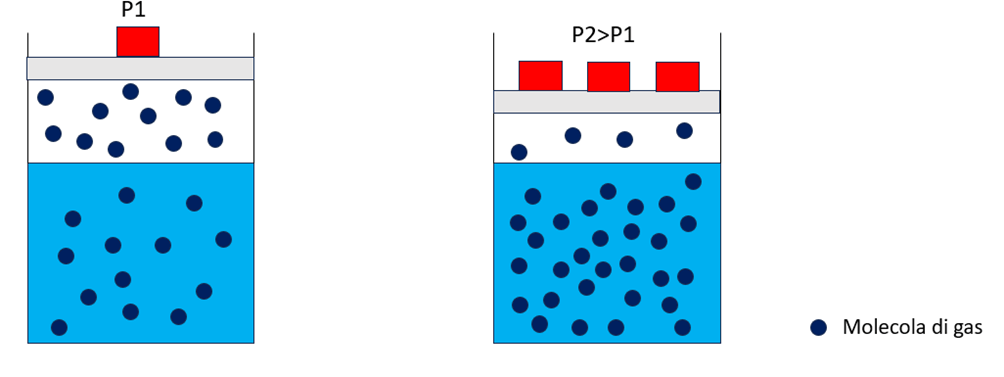
Figura 1 – Dipendenza della solubilità del gas nel liquido al variare della pressione

Anche la temperatura gioca un ruolo chiave nel regolare la solubilità di un gas in un liquido. A una data pressione, la solubilità di un gas in un liquido diminuisce all’aumentare della temperatura.

FORMULE PER ESPRIMERE LA LEGGE DI HENRY

Esistono diverse equazioni per esprimere la legge di Henry:

C = kP

In questa espressione, P rappresenta la pressione che il gas esercita sulla superficie del liquido, C la concentrazione del gas nel liquido mentre k è una costante chiamata costante di Henry il cui valore è correlato alla natura del gas, del liquido e dalla temperatura.

Dall’analisi dimensionale si evidenzia come l’unità di misura di questa costante sia pari a mol/(Latm).

P = kx

In questa espressione, P rappresenta la pressione che il gas esercita sulla superficie del liquido, x la frazione molare del gas nel liquido mentre k è la costante di Henry il cui valore è correlato alla natura del gas, del liquido e dalla temperatura.

Dall’analisi dimensionale si evidenzia come l’unità di misura di questa costante sia pari a una pressione (atm).

yP_tot = kx

In questa espressione compare la legge di Dalton delle pressioni parziali. Può essere utilizzata quando in fase aeriforme è presente una miscela di gas.

y rappresenta la frazione molare del gas in fase gassosa, P_tot rappresenta la pressione totale che l’intera miscela di gas esercita sulla superficie del liquido, x la frazione molare del gas nel liquido e k è la costante di Henry il cui valore è correlato alla natura del gas, del liquido e dalla temperatura.

Dall’analisi dimensionale si evidenzia come l’unità di misura di questa costante sia anche in questo caso pari a una pressione (atm).

CONCETTI CHIAVE:

La legge di Henry governa gli equilibri liquidi-gas.
Diminuire la pressione e aumentare la temperatura rendono sfavorevole la solubilizzazione di un gas in un liquido.
Aumentare la pressione e diminuire la temperatura rendono favorevole la solubilizzazione di un gas in un liquido.

COEFFICIENTE DI VAN’T HOFF

Il coefficiente di Van’t Hoff esprime il numero di moli di ioni o particelle che si vengono a generare dalla dissoluzione di una mole di soluto.

La sua formula è la seguente:

i = 1 + 𝝰 (v-1)

𝝰 = grado di dissociazione

v = numero di ioni che si generano per singola molecola disciolta.

Per elettroliti forti si assume 𝝰=1.

Per elettroliti deboli 𝝰 ha un valore compreso tra 0 e 1

CALCOLO DEL COEFFICIENTE DI VAN’T HOFF

In presenza di elettroliti forti, si assume che il grado di dissociazione 𝝰 sia unitario. In questo caso per calcolare il coefficiente di Van’t Hoff, è sufficiente considerare il numero di ioni che si liberano per singola molecola solubilizzata.

NaOH → Na⁺ + OH^–

Da una mole di NaOH disciolta, si ottengono due moli di ioni. Essendo NaOH un elettrolita forte, si assume che 𝝰=1.

i = 1 + 1 · (2-1) = 2

Na₂SO₄ → 2Na⁺ + SO₄²^–

Da una mole di Na₂SO₄ disciolta, si ottengono tre moli di ioni. Anche in questo caso si ha un elettrolita forte e pertanto 𝝰=1.

i = 1 + 1 · (3-1) = 3

CONCETTI CHIAVE:

Il coefficiente di Van’t Hoff esprime il numero di ioni o particelle che si vengono a generare dalla dissoluzione di una molecola di soluto.
Il coefficiente di Van’t Hoff è correlato al grado di dissociazione 𝝰.
Per elettroliti forti il grado di dissociazione è uguale a 1.
Per elettroliti deboli 0<𝝰<1.

ESERCIZIO SVOLTO:

Si assuma un elettrolita debole di formula bruta X₂Y₃, avente grado di dissociazione 𝝰 = 0,67.

Calcolare il coefficiente di Van’t Hoff.

Guardando la formula bruta del composto è possibile affermare che v sia uguale a 5.

Pertanto:

i = 1 + 0,67 · (5-1) = 3,68

IL REAGENTE LIMITANTE

Il reagente limitante è quello che si consuma completamente nel corso della reazione determinando la quantità di prodotti che si possono ottenere.

Per determinare il reagente limitante, è sufficiente dividere il numero di moli iniziali di ciascun reagente, per il rispettivo coefficiente stechiometrico.

Il reagente, il cui rapporto dà come risultato il valore più basso, rappresenta il reagente limitante.

Il reagente, il cui rapporto dà come risultato il valore più alto, rappresenta il reagente in eccesso.

Se i rapporti danno esattamente come risultato lo stesso valore, allora i reagenti sono presenti in quantità stechiometrica.

CALCOLO DEL REAGENTE LIMITANTE

Si consideri una generica reazione in cui si assuma che la specie A sia il reagente limitante:

aA + bB → rR + sS

A, B, C, D sono le specie chimiche coinvolte nella reazione.

a, b, r, s sono i coefficienti stechiometrici della reazione.

$Calcolo\;reagente\;limitante\;A = \frac{n\; moli\;A}{a}$

$Calcolo\;reagente\;limitante\;B = \frac{n\; moli\;B}{b}$

Se la specie chimica A è il reagente limitante allora:

$\frac{n\; moli\;A}{a}< \frac{n\; moli\;B}{b}$

REAGENTE IN ECCESSO E MOLI DI PRODOTTI

Dalle seguenti formule è possibile ricavare il numero di moli in eccesso di reagente e il numero di prodotti ottenuti:

$n\;moli\;in\;eccesso\;di\;B = n\;moli\;iniziali\;B -(b\cdot\frac{n\; moli\;A}{a})$

$n\;moli\;di\;R = r \cdot \frac{n\; moli\;A}{a}$

$n\;moli\;di\;S = s \cdot \frac{n\; moli\;A}{a}$

ESERCIZIO SVOLTO N.1

Si prenda la seguente reazione già bilanciata:

Ca + 2HCl → CaCl₂ + H₂

Si considerino inizialmente presenti 0,250 moli di calcio metallico e 0,400 moli di acido cloridrico.

Si determini il reagente limitante, il numero di moli di prodotti ottenuti, e il numero di moli in eccesso dell’altro reagente.

Il calcolo del reagente limitante avviene in accordo con le seguenti formule:

$Reagente\;Ca = \frac{n\;moli\;iniziali\;Ca}{1}=\frac{0,250\; moli}{1} = 0,250\;moli$

$Reagente\;HCl = \frac{n\;moli\;iniziali\;HCl}{2}=\frac{0,400\; moli}{2} = 0,200\;moli$

Il valore più basso determina come HCl sia il reagente limitante.

Si procede poi al calcolo del numero di moli di prodotti ottenuti:

$n\;moli\;di\;CaCl_{2} = 1 \cdot 0,200\;moli = 0,200\;moli$

$n\;moli\;di\;H_{2} = 1 \cdot 0,200\;moli = 0,200\;moli$

Il numero di moli in eccesso di calcio si ottiene:

$n\;moli\;in\;eccesso\;di\;Ca = 0,250-1\cdot0,200=0,050 \;moli$

ESERCIZIO SVOLTO N.2

10 g di ossido di calcio vengono sciolti in 300 ml di soluzione 0,2 M di acido fosforico. Dalla reazione si ottengono fosfato di calcio e acqua.

Scrivere la reazione chimica bilanciata.
Determinare il numero di moli iniziali di ciascun reagente.
Determinare il reagente limitante.
Determinare il numero di moli di prodotti ottenuti.
Determinare il numero di moli in eccesso dell’altro reagente una volta completata la reazione.

Punto 1.

Ossido di calcio = CaO

Acido fosforico = H₃PO₄

Fosfato di calcio = Ca₃(PO₄)₂

Acqua = H₂O

3CaO + 2H₃PO₄ → Ca₃(PO₄)₂ + 3H₂O

Punto 2.

Calcolo del numero di moli iniziali:

$n\;moli\;CaO = \frac{10,00\;g}{56,08\;g/mol} = 0,178\;moli$

$n\;moli\;H_{3}PO_{4} = 0,300\;L\cdot0,2\;mol/L = 0,060\;moli$

Punto 3.

Calcolo del reagente limitante:

$Reagente\;CaO = \frac{n\;moli\;iniziali\;CaO}{2}=\frac{0,178\; moli}{3} = 0,059\;moli$

$Reagente\;H_{3}PO_{4} = \frac{n\;moli\;iniziali\;H_{3}PO_{4}}{3}=\frac{0,060\; moli}{2} = 0,030\;moli$

H₃PO₄ è il reagente limitante.

Punto 4.

Calcolo dei prodotti ottenuti:

$n\;moli\;di\;Ca_{3}(PO_{4})_2 = 1 \cdot 0,030\;moli = 0,030\;moli$

$n\;moli\;di\;H_{2}O = 3 \cdot 0,030\;moli = 0,090\;moli$

Punto 5.

Calcolo dell’eccesso di reagente:

$n\;moli\;in\;eccesso\;di\;CaO = 0,178-3\cdot0,030=0,088 \;moli$

SOLUZIONI TAMPONE

Le soluzioni tampone sono miscele di acidi o basi deboli con sali che permettono di opporsi a grosse variazioni di pH in caso di aggiunte modeste di acido forte o base forte.

Le soluzioni tampone possono essere costituite da:

Un acido debole e un sale contenente la base coniugata dell’acido debole.
Una base debole e un sale contenente l’acido coniugato della base debole.

Le soluzioni tampone prendono questo nome in quanto dotate di potere tamponante che viene calcolato come la quantità di acido forte o base forte che deve essere aggiunto per avere la variazione di 1 unità di pH.

Per il calcolo del pH di una soluzione tampone è possibile utilizzare l’equazione di Henderson-Hasselbach.

AZIONE TAMPONANTE SISTEMA ACIDO DEBOLE/BASE CONIUGATA

Per una soluzione contenente acido acetico (acido debole) e acetato di sodio (sale) è possibile scrivere le seguenti reazioni:

CH₃COOH ⇄ H⁺ + CH₃COO^–

CH₃COONa → Na⁺ + CH₃COO^–

L’addizione del sale è fondamentale per avere una quantità maggiore di acetato (CH₃COO^– ) che altrimenti si otterrebbe in porzioni ridottissime solo dalla dissociazione dell’acido acetico.

Nel caso di addizione di un acido forte come HCl, tale acido viene immediatamente neutralizzato dallo ione acetato in accordo con la seguente reazione:

H⁺ + CH₃COO^– → CH₃COOH

Nel caso di addizione di una base forte come NaOH, tale base viene immediatamente neutralizzata dall’acido acetico in accordo con la seguente reazione:

OH^– + CH₃COOH → CH₃COO^– + H₂O

AZIONE TAMPONANTE SISTEMA BASE DEBOLE/ACIDO CONIUGATO

Per una soluzione contenente ammoniaca (base debole) e cloruro di ammonio (sale) è possibile scrivere le seguenti reazioni:

NH₃ + H₂O ⇄ NH₄⁺ + OH^–

NH₄Cl → NH₄⁺ + Cl^–

L’addizione del sale è fondamentale per avere una quantità maggiore di ammonio (NH₄⁺) che altrimenti si otterrebbe in misura ridottissima solo dall’idrolisi dell’ammoniaca.

Nel caso di addizione di un acido forte come HCl, tale acido viene immediatamente neutralizzato dall’ammoniaca in accordo con la seguente reazione:

H⁺ + NH₃ → NH₄⁺

Nel caso di addizione di una base forte come NaOH, tale base viene immediatamente neutralizzata dallo ione ammonio in accordo con la seguente reazione:

OH^– + NH₄⁺ → NH₃ + H₂O

CONCETTI CHIAVE:

Una soluzione tampone è in grado di opporsi a grosse variazioni di pH in caso di aggiunte modeste di acido forte o base forte.
Una soluzione tampone può essere costituita da un acido debole e dal sale contenente la sua base coniugata.
Una soluzione tampone può essere costituita da una base debole e dal sale contenente il suo acido coniugato.

ESERCIZIO SVOLTO:

Calcolare il pH di 50 ml di soluzione contenente acido formico HCOOH in concentrazione 0,1 M e formiato di sodio NaHCOO 0,1 M. (K_a=1,77 · 10^-4)

Come varia il pH dopo l’aggiunta di 10 ml di una soluzione 0,05M di KOH?

Il sistema acido formico-formiato di sodio rappresenta un esempio di soluzione tampone. Le reazioni in acqua sono le seguenti:

HCOOH ⇄ H⁺ + CH₃COO^–

HCOONa → Na⁺ + HCOO^–

Si assuma che l’acido formico sia sufficientemente debole da considerare la quantità dissociata trascurabile rispetto a quella presente inizialmente. Inoltre, per il principio di Le Chatelier, la quantità di HCOO^– derivante dalla dissociazione del sale inibisce ulteriormente la dissociazione dell’acido.

[HCOOH] = 0,1 M
[HCOO^–] = 0,1 M

Il pH può essere calcolato in accordo con l’equazione di Henderson-Hasselbach:

$pH = pK_{a} + log_{10}\frac{[HCOO^{-}]}{[HCOOH]}$

Occorre per prima cosa calcolare il valore di pK_a:

pK_a = -log₁₀K_a = -log₁₀(1,77 · 10^-4) = 3,75

Pertanto:

$pH = pK_{a} + log_{10}\frac{0,1}{0,1}= pK_{a} = 3,75$

Aggiunta di 10 ml di una soluzione 0,05M di KOH.

Essendo KOH una base forte e completamente dissociata è possibile scrivere la reazione con l’acido formico:

OH^– + HCOOH → HCOO^– + H₂O

Il numero moli iniziali di ciascun reagente può essere calcolato:

n moli iniziali HCOOH = 0,050 L · 0,1 mol/L = 5,00 · 10^-3 mol

n moli iniziali OH^– = 0,010 L · 0,05 mol/L = 5,00 · 10^-4 mol

n moli iniziali HCOO^– = 0,050 L · 0,1 mol/L = 5,00 · 10^-3 mol

Il decorso della reazione può essere descritto dalla tabella:

	n moli HCOOH	n moli OH^–	n moli HCOO^–
t₀ (n moli iniziali)	5,00 · 10^-3	5,00 · 10^-4	5,00 · 10^-3
n moli che reagiscono	-5,00 · 10^-4	-5,00 · 10^-4	+5,00 · 10^-4
n moli all’equilibrio (t₀-reagite)	4,50 · 10^-3	0	5,50 · 10^-3

Il volume totale della soluzione è la somma del volume iniziale e di quello aggiunto contenente la base.

V_totale = (50 +10) ml = 60 ml

Il pH può essere calcolato ancora una volta con l’equazione di Henderson-Hasselbach:

$pH = pK_{a} + log_{10}\frac{[HCOO^{-}]}{[HCOOH]}$

$pH = 3,75 + log_{10}\frac{\frac{5,50\cdot10^{-3}\;moli}{60 \;ml}}{\frac{4,50\cdot10^{-3}\;moli}{60\; ml}}= 3,75\;+\;0,09 = 3,84$

Da osservare come il volume totale di 60 ml compaia sia al numeratore che al denominare nell’equazione di Henderson-Hasselbach, e pertanto può essere semplificato.

Inoltre la variazione del pH è di appena 0,09 unità di pH rispetto al valore iniziale di 3,75 sottolineando come l’effetto tampone sia ben marcato.

EQUAZIONE DI HENDERSON-HASSELBACH

L’equazione di Henderson-Hasselbach si utilizza per il calcolo del pH in soluzioni tampone contenenti:

Un acido debole e la base coniugata dell’acido debole.
Una base debole e l’acido coniugato della base debole.

L’equazione può essere scritta come:

$pH = pK_{a} + log_{10}\frac{C_{b}}{C_{a}}$

$pOH = pK_{b} + log_{10}\frac{C_{a}}{C_{b}}$

K_aè la costante di dissociazione acida.
K_b è la costante di dissociazione basica.

ACIDO DEBOLE E BASE CONIUGATA DELL’ACIDO DEBOLE

Per una soluzione contenente acido acetico e acetato di sodio è possibile scrivere le seguenti reazioni:

CH₃COOH ⇄ H⁺ + CH₃COO^–

CH₃COONa → Na⁺ + CH₃COO^–

Questo sistema rappresenta un valido esempio di sistema tampone e il calcolo del pH è espresso dall’equazione di Henderson-Hasselbach:

$pH = pK_{a} + log_{10}\frac{[CH_{3}COO^{-}]}{[CH_{3}COOH]}$

Se [CH₃COOH] = [CH₃COO^–] allora:

$pH = pK_{a} + log_{10}1 = pK_{a}$

Pertanto, è possibile affermare che:

Se [CH₃COOH] > [CH₃COO^–] allora pH < pK_a
Se [CH₃COOH] = [CH₃COO^–] allora pH = pK_a
Se [CH₃COOH] < [CH₃COO^–] allora pH > pK_a

BASE DEBOLE E ACIDO CONIUGATO DELLA BASE DEBOLE

Per una soluzione contenente ammoniaca e cloruro d’ammonio è possibile scrivere le seguenti reazioni:

NH₃ + H₂O ⇄ NH₄⁺ + OH^–

NH₄Cl → NH₄⁺ + Cl^–

Questo sistema rappresenta un valido esempio di sistema tampone e il calcolo del pH è espresso dall’equazione di Henderson-Hasselbach:

$pOH = pK_{b} + log_{10}\frac{[NH_{4}^{+}]}{[NH_{3}]}$

$pH = pK_{a} + log_{10}\frac{[NH_{3}]}{[NH_{4}^{+}]}$

Nel caso si scelga di utilizzare la prima equazione, per il calcolo del pH occorre ricordare la seguente relazione:

pH + pOH = 14

Nel caso si scelga di utilizzare la seconda equazione, per il calcolo di pK_a occorre ricordare la seguente relazione:

pK_a + pK_b = 14

Come dimostrato nell’esercizio svolto sotto, entrambe le strade sono equivalenti e portano alla fine lo stesso valore di pH.

Se [NH₃] = [NH₄⁺] allora:

$pOH = pK_{b} + log_{10}1 = pK_{b}$

$pH = pK_{a} + log_{10}1 = pK_{a}$

Pertanto, è possibile affermare che:

Se [NH₃] > [NH₄⁺] allora pOH < pK_be pH > pK_a
Se [NH₃] = [NH₄⁺] allora pOH = pK_be pH = pK_a
Se [NH₃] < [NH₄⁺] allora pOH > pK_be pH < pK_a

CONCETTI CHIAVE:

L’equazione di Henderson-Hasselbach può essere utilizzata per il calcolo del pH in soluzioni tampone.
L’equazione può avere due forme a seconda se si voglia calcolare il pH o il pOH.
Le due forme portano comunque alla fine a ottenere lo stesso valore di pH.

ESERCIZIO SVOLTO:

Calcolare il pH di una soluzione contenente NH₃in concentrazione 0,5 M e NH₄Cl in concentrazione 0,3M. Si assuma che K_bdell’ammoniaca sia uguale a 1,75 · 10^-5.

Per una soluzione contenente ammoniaca e cloruro d’ammonio è possibile scrivere le seguenti reazioni:

NH₃ + H₂O ⇄ NH₄⁺ + OH^–

NH₄Cl → NH₄⁺ + Cl^–

Dal momento che l’ammoniaca è una base debole, si assume che la quantità dissociata sia trascurabile rispetto a quella iniziale.

Pertanto:

[NH₃] = 0,5 M
[NH₄⁺] = 0,3 M

Per prima cosa occorre calcolare il valore di K_b che è uguale a:

K_b = -log₁₀K_b = -log₁₀(1,75 · 10^-5) = 4,76

$pOH = pK_{b} + log_{10}\frac{[NH_{4}^{+}]}{[NH_{3}]}= 4,76 + log_{10}\frac{0,3}{0,5} = 4,54$

$pH = 14,00 - 4,54 = 9,46$

Nel caso si scelga di utilizzare la seguente forma dell’equazione di Henderson-Hasselbach:

$pH = pK_{a} + log_{10}\frac{[NH_{3}]}{[NH_{4}^{+}]}$

Occorre calcolare il valore di pKa:

$pK_{a} = 14,00 - 4,76 = 9,24$

$pH = 9,24 + log_{10}\frac{0,5}{0,3}=9,46$

É dimostrato che le due forme dell’equazione di Henderson-Hasselbach portano al medesimo risultato.

CALCOLO DEL pH (basi deboli)

Una base debole si dissocia solo parzialmente in acqua. Per il calcolo del pH occorre tenere conto della sua costante di dissociazione basica (K_b) e della sua concentrazione in soluzione.

Esistono due formule per il calcolo:

Una semplificata che si applica per basi molto deboli e concentrate in soluzione.
Una estesa che si applica nei casi in cui quella semplificata non è applicabile.

Dissociazione della base debole

Si consideri la reazione di idrolisi dell’ammoniaca NH₃ in acqua:

NH₃ + H₂O ⇄ NH₄⁺+ OH^–

La costante di dissociazione basica è espressa dalla seguente formula:

$K_{b}= \frac{[NH_{4}^{+}][OH^{-}]}{[NH_{3}]}$

Dalla stechiometria della reazione si evince che per ogni mole di NH₃ che reagisce, si ottiene una mole di NH₄⁺e una mole di OH^–.

Il decorso della reazione può essere descritto dai seguenti passaggi:

Al tempo zero t₀ è presente solo l’ammoniaca NH₃.
La quantità di NH₃ che reagisce si indica come -x
La quantità di NH₄⁺e di OH^– che si ottengono dalla reazione si indicano come +x.

Si consideri una soluzione contenente ammoniaca in concentrazione 0,1 M. Il decorso della reazione può essere descritto come:

	[NH₃] (mol/L)	[NH₄⁺] (mol/L)	[OH^–] (mol/L)
t₀	0,1	0	0
Quantità che reagisce	-x	+x	+x
Concentrazione all’equilibrio	0,1 – x	+x	+x

La formula della costante d’equilibrio K_bpuò essere riscritta come:

$K_{b}= \frac{[NH_{4}^{+}][OH^{-}]}{[NH_{3}]}=\frac{(+x)(+x)}{(0,1-x)}$

Calcolo del pH con la formula semplificata

Se la base è molto debole ed è presente in quantità abbastanza concentrata, la quantità -x è trascurabile rispetto alla concentrazione iniziale.

Pertanto:

$K_{b}= \frac{(+x)(+x)}{(0,1-x)}=\frac{(+x)(+x)}{(0,1)}$

Posto x = [OH^–].

$x = \sqrt{0,1\cdot K_{b}}$

Per l’ammoniaca il valore di K_b = 1,75 · 10^-5

$[OH^{-}] = \sqrt{0,1\cdot 1,75\cdot 10^{-5}}=1,32\cdot 10^{-3}M$

$pOH = -log_{10}(1,32\cdot 10^{-3}) = 2,88$

$pH = 14-pOH = 11,12$

La formula per esprimere il pH, nel caso si utilizzi la formula semplificata, è la seguente:

$pH = 14-(-log_{10}\sqrt{K_{b}\cdot C_{b}})$

Calcolo del pH con la formula estesa

Nel calcolo esteso non si considera più -x trascurabile rispetto alla concentrazione iniziale di ammoniaca.

Pertanto:

$K_{b}= \frac{(+x)(+x)}{(0,1-x)}$

$K_{b}\cdot(0,1-x)= x^{2}$

$1,75\cdot10^{-5}\cdot(0,1-x)= x^{2}$

$1,75\cdot10^{-6}-1,75\cdot10^{-5}x= x^{2}$

$x^{2}+1,75\cdot10^{-5}x-1,75\cdot10^{-6}= 0$

$\Delta = (1,75\cdot10^{-5})^{2}-4\cdot(1)\cdot(-1,75\cdot10^{-6})= 7,00 \cdot10^{-6}$

Dal momento che la concentrazione di ioni OH^– non può essere negativa:

$x = \frac{-1,75\cdot 10^{-5}+ \sqrt{7,00\cdot 10^{-6}}}{2}=1,31\cdot 10^{-3}M$

$pOH = -log_{10}(1,31\cdot 10^{-3}) = 2,88$

$pH = 14-pOH = 11,22$

Dai calcoli si evidenzia come i valori di pH ottenuti dai due procedimenti siano identici. Questo perché l’ammoniaca è una base molto debole ed è presente in quantità abbastanza concentrata.

CONCETTI CHIAVE:

Il calcolo del pH di una base debole prevede un calcolo più complesso rispetto a quello di un acido forte.
La formula semplificata si può applicare in caso di basi molto deboli e se presenti in quantità abbastanza concentrata.
La formula estesa può essere usata sempre, soprattutto nei casi in cui la formula semplificata non può essere adottata.

ESERCIZIO SVOLTO:

Calcolare il pH di una soluzione contenente anilina C₆H₅NH₂ 0,01 M. (K_b = 3,82 · 10^-10).

Si utilizzi solo la formula semplificata.

La reazione di idrolisi della base può essere scritta come:

C₆H₅NH₂ + H₂O ⇄ C₆H₅NH₃⁺ + OH^–

Il calcolo del pH, quando si utilizza la formula semplificata, è il seguente:

$pH = 14-(-log_{10}\sqrt{K_{b}\cdot C_{b}})$

$pH = 14-(-log_{10}\sqrt{3,82\cdot10^{-10}\cdot 0,01})=8,29$

CALCOLO DEL pH (acidi deboli)

Un acido debole si dissocia solo parzialmente in acqua. Per il calcolo del pH occorre tenere conto della sua costante di dissociazione acida (K_a) e della sua concentrazione in soluzione.

Esistono due formule per il calcolo:

Una semplificata che si applica per acidi molto deboli e concentrati in soluzione.
Una estesa che si applica nei casi in cui quella semplificata non è applicabile.

Dissociazione dell’acido debole

Si consideri la reazione di dissociazione dell’acido acetico CH₃COOH in acqua:

CH₃COOH ⇄ H⁺+ CH₃COO^–

La costante di dissociazione è espressa dalla seguente formula:

$K_{a}= \frac{[H^{+}][CH_{3}COO^{-}]}{[CH_{3}COOH]}$

Dalla stechiometria della reazione si evince che per ogni mole di CH₃COOH che reagisce, si ottiene una mole di H⁺e una mole di CH₃COO^–.

Il decorso della reazione può essere descritto dai seguenti passaggi:

Al tempo zero t₀ è presente solo l’acido acetico CH₃COOH.
La quantità di CH₃COOH che reagisce si indica come -x
La quantità di H⁺e di CH₃COO^– che si ottengono dalla reazione si indicano come +x.

Si consideri una soluzione contenente acido acetico in concentrazione 0,1 M. Il decorso della reazione può essere descritto come:

	[CH₃COOH] (mol/L)	[H⁺] (mol/L)	[CH₃COO^–] (mol/L)
t₀	0,1	0	0
Quantità che reagisce	-x	+x	+x
Concentrazione all’equilibrio	0,1 – x	+x	+x

La formula della costante d’equilibrio K_apuò essere riscritta come:

$K_{a}= \frac{[H^{+}][CH_{3}COO^{-}]}{[CH_{3}COOH]}=\frac{(+x)(+x)}{(0,1-x)}$

Calcolo del pH con la formula semplificata

Se l’acido è molto debole ed è presente in quantità abbastanza concentrata, la quantità -x è trascurabile rispetto alla concentrazione iniziale.

Pertanto:

$K_{a}= \frac{(+x)(+x)}{(0,1-x)}=\frac{(+x)(+x)}{(0,1)}$

Posto x = [H⁺].

$x = \sqrt{0,1\cdot K_{a}}$

Per l’acido acetico K_a = 1,75 · 10^-5

$[H^{+}] = \sqrt{0,1\cdot 1,75\cdot 10^{-5}}=1,32\cdot 10^{-3}M$

$pH = -log_{10}(1,32\cdot 10^{-3}) = 2,88$

La formula per esprimere il pH, nel caso si utilizzi la formula semplificata, è la seguente:

$pH = -log_{10}\sqrt{K_{a}\cdot C_{a}}$

Calcolo del pH con la formula estesa

Nel calcolo esteso non si considera più -x trascurabile rispetto alla concentrazione iniziale di acido acetico.

Pertanto:

$K_{a}= \frac{(+x)(+x)}{(0,1-x)}$

$K_{a}\cdot(0,1-x)= x^{2}$

$1,75\cdot10^{-5}\cdot(0,1-x)= x^{2}$

$1,75\cdot10^{-6}-1,75\cdot10^{-5}x= x^{2}$

$x^{2}+1,75\cdot10^{-5}x-1,75\cdot10^{-6}= 0$

$\Delta = (1,75\cdot10^{-5})^{2}-4\cdot(1)\cdot(-1,75\cdot10^{-6})= 7,00 \cdot10^{-6}$

Dal momento che la concentrazione di ioni H⁺ non può essere negativa:

$x = \frac{-1,75\cdot 10^{-5}+ \sqrt{7,00\cdot 10^{-6}}}{2}=1,31\cdot 10^{-3}M$

$pH = -log_{10}(1,31\cdot 10^{-3}) = 2,88$

Dai calcoli si evidenzia come i valori di pH ottenuti dai due procedimenti siano identici. Questo perché l’acido acetico è un acido molto debole ed è presente in quantità abbastanza concentrata.

CONCETTI CHIAVE:

Il calcolo del pH di un acido debole prevede un calcolo più complesso rispetto a quello di un acido forte.
La formula semplificata si può applicare in caso di acidi molto deboli e se presenti in quantità abbastanza concentrata.
La formula estesa può essere usata sempre, soprattutto nei casi in cui la formula semplificata non può essere adottata.

ESERCIZIO SVOLTO:

Calcolare il pH di una soluzione contenente HCOOH 0,5 M. (K_a = 1,77 · 10^-4).

Si utilizzi solo la formula semplificata.

La reazione di dissociazione dell’acido può essere scritta come:

HCOOH ⇄ H⁺ + HCOO^–

La formula per esprimere il pH, quando si utilizza la formula semplificata, è la seguente:

$pH = -log_{10}\sqrt{K_{a}\cdot C_{a}}$

$pH = -log_{10}\sqrt{1,77\cdot10^{-4}\cdot 0,5}=2,03$

CALCOLO DEL pH (acidi forti e basi forti)

Acido forte

Per una soluzione contenente un acido forte, in concentrazione superiore a 10^-5M, la concentrazione di ioni H⁺ coincide con la concentrazione dell’acido in soluzione.

Se si indica la concentrazione dell’acido come C_a, il calcolo del pH diventa:

pH = -log₁₀C_a

Se la concentrazione dell’acido è inferiore a 10^-5 M occorre considerare il comportamento di questo acido come debole.

Base forte

Per una soluzione contenente una base forte, in concentrazione superiore a 10^-5M, la concentrazione di ioni OH^– coincide con la concentrazione della base in soluzione.

Se si indica la concentrazione della base come C_b, il calcolo del pOH diventa:

pOH = -log₁₀C_b

Pertanto il calcolo del pH è il seguente:

pH = 14 – (-log₁₀C_b)

Se la concentrazione della base è inferiore a 10^-5 M occorre considerare il comportamento di questa base come debole.

CONCETTI CHIAVE:

Per una soluzione contenente un acido forte, in concentrazione superiore a 10^-5M, la concentrazione di ioni H⁺ coincide con la concentrazione dell’acido in soluzione.
Per una soluzione contenente una base forte, in concentrazione superiore a 10^-5M, la concentrazione di ioni OH^– coincide con la concentrazione della base in soluzione.

ESERCIZIO SVOLTO:

Calcolare il pH di una soluzione contenente NaOH 0,2 M.

NaOH è nell’elenco delle basi forti e questa si dissocia completamente in accordo con la seguente reazione:

NaOH → Na⁺ + OH^–

La concentrazione di ioni OH^– coincide con la concentrazione della base.

[OH^–] = 0,2 M

Pertanto:

pOH = -log₁₀(0,2) = 0,70

pH = 14,00 – 0,70 = 13,30

SALI BINARI

I sali binari sono composti binari che hanno formula MX e costituiti da:

M che è un metallo avente numero d’ossidazione positivo.
X che è un non metallo avente numero d’ossidazione negativo.

Anche i sali di ammonio (NH₄⁺), aventi formula NH₄X, seguono le regole di nomenclatura dei sali binari.

Nella formula dei sali binari, il metallo compare sempre come primo mentre il non metallo come secondo.

NOMENCLATURA SALI BINARI

NOMENCLATURA IUPAC

La nomenclatura IUPAC prevede di nominare i composti seguendo la regola dell’incrocio, partendo dal composto che compare come secondo e poi citando quello che compare come primo. Ciascun elemento è accompagnato da un prefisso che identifica in maniera univoca il numero di atomi che lo costituisce.

La formula per costruire il nome di un sale binario è il seguente:

Prefisso + Nome del non metallo + uro + di + Prefisso + Nome del metallo

MgBr₂ – Dibromuro di magnesio

Fe₂S₃ – Trisolfuro di diferro

PdF₄ – Tetrafluoruro di palladio

ZnI₂ – Diidruro di zinco

CuCl – Cloruro di rame

(NH₄)₂S – Solfuro di diammonio

NOMENCLATURA TRADIZIONALE

La nomenclatura tradizionale non prevede l’utilizzo di prefissi. In presenza di metalli con due stati di ossidazione, a quello avente numero d’ossidazione più basso si aggiunge il suffisso oso, mentre a quello con più alto numero d’ossidazione si aggiunge il suffisso ico.

CuF₂ – Fluoruro rameico.

NaI – Ioduro di sodio

NiS – Solfuro nicheloso

FeCl₃ – Cloruro ferrico

HgBr₂ – Bromuro mercurico

NOTAZIONE DI STOCK

La notazione di Stock si utilizza solo in presenza di metalli che presentano più numeri di ossidazione. Si utilizza il seguente schema:

NOME DEL NON METALLO + uro + di METALLO (stato d’ossidazione del metallo in numero romano)

Alcuni esempi:

FeBr₃ – Bromuro di ferro (III)

CoSe – Seleniuro di cobalto (II)

Ni₃N₂ – Nitruro di nichel (II)

HgI₂ – Ioduro di mercurio (II)

CONCETTI CHIAVE:

I sali binari hanno formula MX (metallo + non metallo) in cui il metallo ha numero d’ossidazione positivo mentre il non metallo negativo.
Nella formula chimica dei sali binari, il metallo compare sempre come primo e il non metallo come secondo.

ESERCIZIO SVOLTO 1:

Nominare il seguente composto seguendo le regole della nomenclatura IUPAC, tradizionale e notazione di Stock:

Bi₂Te₃

La nomenclatura IUPAC prevede di nominare prima il tellurio e poi il bismbuto (regola dell’incrocio) ciascun preceduto dal prefisso che ne identifica il numero di atomi.

Bi₂Te₃ – Tritelluriuro di dibismuto

La nomenclatura tradizionale prevede di nominare prima il tellurio e poi il bismuto (regola dell’incrocio) senza alcun prefisso che ne identifichi il numero di atomi. In presenza di più numeri d’ossidazione del metallo, quello più basso è accompagnato dal suffisso oso, mentre quello più alto dal suffisso ico.

Nel composto Bi₂Te₃, il tellurio ha numero d’ossidazione negativo mentre il bismuto ha numero d’ossidazione positivo. Guardando la tavola periodica, si osserva come il tellurio abbia come unico numero d’ossidazione negativo -2, mentre il bismuto abbia numeri d’ossidazione +3 e +5. Per il principio dell’elettroneutralità, il bismuto deve avere come numero d’ossidazione +3. Pertanto, il suffisso da attribuire al metallo in questo caso è oso.

Bi₂Te₃ – Telluriuro bismutoso

La notazione di Stock prevede nel formulare il nome, l’utilizzo del seguente schema:

NOME DEL NON METALLO + uro + di METALLO (stato d’ossidazione del metallo in numero romano)

Bi₂Te₃ – Telluriuro di bismuto (III)

ESERCIZIO SVOLTO 2:

Determinare la formula del seguente composto:

FOSFURO STANNICO

Il composto rientra nella categoria dei sali binari ed è costituito da un non metallo, fosforo, avente numero d’ossidazione negativo, e dal metallo stagno avente numero d’ossidazione positivo. Guardando la tavola periodica, si evidenzia come lo stagno appartenga al gruppo IVA e abbia come numeri di ossidazione +2 e +4, mentre il fosforo abbia come unico numero d’ossidazione negativo -3. Il suffisso ico indica che il metallo ha il numero d’ossidazione positivo più alto, ovvero +4.

Essendo il composto nel complesso neutro, esso deve essere costituito da quattro atomi di fosforo (carica complessiva -12) e tre di stagno (carica complessiva +12):

Sn₃P₄

ELETTROLITI E NON ELETTROLITI

ELETTROLITI

Gli elettroliti sono sostanze che disciolte in acqua si dissociano o ionizzano per dare ioni aventi carica opposta. Queste soluzioni contengono cariche libere di muoversi e per questo conducono corrente elettrica. Una buona indicazione della forza di un elettrolita è data dal grado di dissociazione.

Gli elettroliti si definiscono forti quando in soluzione si dissociano completamente. Rientrano in questa categoria:

I sali (ad eccezione di alcuni sali di cadmio come il CdSO₄)
Le basi forti
Gli acidi forti.

Alcuni esempi di reazione in acqua di elettroliti forti:

NaOH → Na⁺ + OH^– (Base forte)

HCl → H⁺ + Cl^– (Acido forte)

NaCl → Na⁺ + Cl^– (Sale)

Gli elettroliti deboli sono sostanze che si dissociano solo parzialmente in acqua. Essi sono:

Acidi deboli.
Basi deboli.

Alcuni esempi di reazione in acqua di elettroliti deboli

CH₃COOH + H₂O ⇄ CH₃COO^–+ H₃O⁺ (Acido debole)

NH₃ + H₂O ⇄ NH₄⁺+ OH^– (Base debole)

NON ELETTROLITI

I non elettroliti sono sostanze che in acqua non si dissociano e non liberano ioni di carica opposta. Un esempio è il glucosio.

Dal momento che non sono presenti cariche libere di muoversi queste soluzione non conducono corrente elettrica.

CONCETTI CHIAVE:

Gli elettroliti sono sostanze che in acqua si dissociano o ionizzano per dare ioni di carica opposta.
Gli elettroliti forti sono sostanze che si dissociano o ionizzano completamente.
Gli elettroliti deboli sono sostanze che si dissociano o ionizzano solo parzialmente.
I non elettroliti in acqua non danno ioni aventi carica opposta.