Categoria: Teoria

IDROLISI SALINA

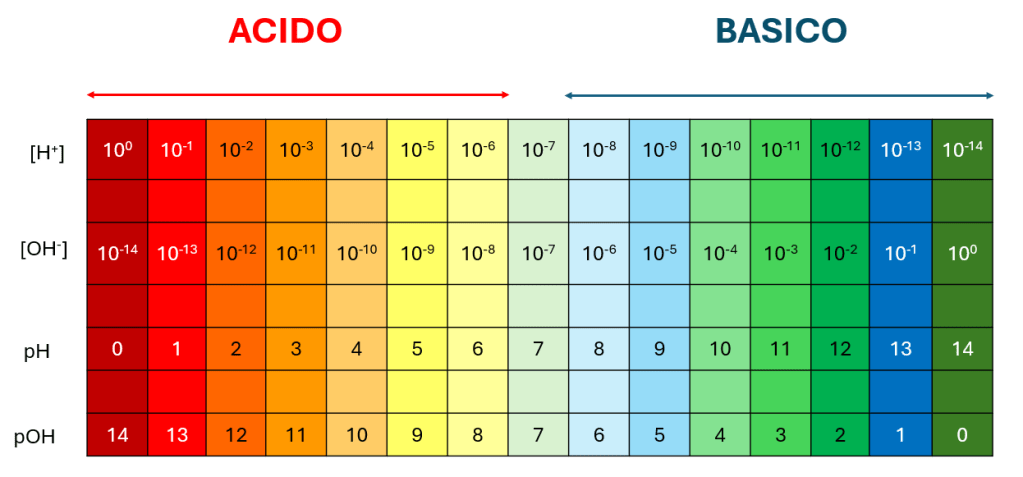
L’idrolisi salina è un fenomeno chimico in cui un sale disciolto in acqua è in grado di modificare il pH della soluzione.

Ciò è dovuto alla presenza di ioni che reagendo con l’acqua aumentano la concentrazione di ioni H+ e spostano il pH verso valori più acidi (idrolisi acida), o alla presenza di ioni che incrementano la concentrazione di ioni OH– e rendono il pH più basico (idrolisi basica).

  • L’idrolisi salina basica avviene quando l’anione del sale è la base coniugata di un acido debole.
  • L’idrolisi salina acida avviene quando il catione del sale è l’acido coniugato di una base debole.
  • Non avviene idrolisi salina quando sia il catione che l’anione, reagendo in acqua, formerebbero un acido forte e una base forte.

IDROLISI BASICA

Si consideri la solubilizzazione dell’acetato di sodio in acqua:

CH3COONa → Na+ + CH3COO–

Dalla reazione, che giunge a completamento, si liberano gli ioni Na+ e CH3COO–.

Lo ione Na+ non può reagire in acqua in quanto si otterrebbe da tale reazione la base forte NaOH. L’equilibrio di questa reazione è spostato completamente verso i reagenti.

Na+ + H2O ⇄ NaOH + H+ (NON AVVIENE!!!)

Lo ione CH3COO– è la base coniugata di un acido debole, nello specifico dell’acido acetico CH3COOH.

Lo ione acetato può reagire con l’acqua secondo la seguente reazione:

CH3COO– + H2O ⇄ CH3COOH + OH–

Tale reazione porta a un incremento della concentrazione di ioni OH– in soluzione, e pertanto si ha un incremento nei valori di pH.

Nel complesso, il sale acetato di sodio, una volta sciolto in acqua, rende la soluzione basica.

IDROLISI ACIDA

Si consideri la solubilizzazione del cloruro d’ammonio in acqua:

NH4Cl → NH4+ + Cl–

Dalla reazione, che giunge a completamento, si liberano gli ioni NH4+ e Cl–.

Lo ione ammonio NH4+è l’acido coniugato dell’ammoniaca, che è una base debole in grado di reagire con l’acqua secondo la seguente reazione:

NH4+ + H2O ⇄ NH3 + H3O+

Sapendo che lo ione H3O+ rappresenta lo ione H+ idratato (H++ H2O) è possibile dire che tale reazione comporti lo spostamento del pH verso valori più acidi.

Lo ione cloruro Cl– non è in grado di reagire con l’acqua in quanto rappresenta la base coniugato di un acido forte (HCl).

Cl– + H2O ⇄ HCl + OH– (NON AVVIENE!!!)

L’equilibrio di tale reazione è completamente spostato verso i reagenti.

Nel complesso, il sale cloruro d’ammonio, una volta sciolto in acqua, rende la soluzione acida.

NESSUNA IDROLISI SALINA

La solubilizzazione del cloruro di potassio avviene secondo la seguente reazione:

KCl → K++ Cl–

Nessuno dei due ioni può dare reazioni di idrolisi in quanto si formerebbero KOH e HCl che sono rispettivamente una base e un acido forte:

K+ + H2O ⇄ KOH + H+ (NON AVVIENE!!!)

Cl– + H2O ⇄ HCl + OH– (NON AVVIENE!!!)

Pertanto, sciogliendo il sale KCl in acqua, non si hanno variazioni di pH.

CONCETTI CHIAVE:

  • L’idrolisi salina basica si ha quando l’anione del sale è la base coniugata di un acido debole.
  • L’idrolisi salina acida si ha quando il catione del sale è l’acido coniugato di una base debole.
  • Non si ha idrolisi salina quando sia il catione che l’anione reagendo in acqua, formerebbero un acido forte e una base forte.

AUTOPROTOLISI DELL’ACQUA

La reazione di autoprotolisi o autoionizzazione dell’acqua è una reazione chimica che coinvolge due molecole d’acqua, una delle quali si comporta da acido mentre l’altra da base.

H2O + H2O ⇄ H3O+ + OH–

Dalla reazione si vengono a produrre due specie ioniche che spiegano la lieve conducibilità elettrica posseduta dall’acqua.

LA COSTANTE D’EQUILIBRIO KW

La costante d’equilibrio per descrivere l’equilibrio viene indicata con Kw e può essere descritta dalla seguente relazione:

Kw = [H3O+]·[OH–]

Sapendo che lo ione H3O+ corrisponde allo ione H+ idratato (H++ H2O) è possibile riscrivere la formula della costante d’equilibrio come:

Kw = [H+]·[OH–]

A 25°C il valore di valore Kw è uguale a 1,00 · 10-14.

Ogni reazione di autoprotolisi genera uno ione H+ e uno ione OH–. Si può calcolare:

[H^{+}]=[OH^{-}]=\sqrt{1,00\cdot 10^{-14}}=1,00\cdot 10^{-7}M

Pertanto il valore del pH è uguale a:

pH = -log10(1,00·10-7) = 7,00

CONCETTI CHIAVE:

  • La reazione di autoprotolisi dell’acqua coinvolge due molecole d’acqua una delle quali si comporta da acido mentre l’altra da base.
  • Dalla reazione di autoprotolisi dell’acqua si generano due specie ioniche che spiegano la lieve conducibilità dell’acqua.
  • Il valore di Kw è uguale a 1,00 · 10-14.
  • Il pH dell’acqua pura a 25°C è uguale a 7,00.

TITOLAZIONE BASE FORTE CON ACIDO FORTE

La titolazione di una base forte con un acido forte prevede che vi sia una reazione chimica tra una base forte e un acido forte.

  • La base forte è l’analita, ovvero la sostanza che deve essere titolata.
  • L’acido forte è il titolante, ovvero la sostanza che viene aggiunta all’analita.

Nella curva di titolazione viene graficato il valore del pH al variare del volume di titolante aggiunto.

La titolazione avviene fino al raggiungimento del punto equivalente, in cui la quantità di equivalenti di base eguaglia la quantità di equivalenti di acido.

Titolazione di NaOH con HCl

Si considerino 50 ml di una soluzione 0,1 M di NaOH che vengono titolati con una soluzione 0,1 M di HCl. La reazione può essere descritta come:

NaOH + HCl → H2O + Na+ + Cl–

Essendo NaOH una base forte, il pH iniziale può essere calcolato come:

pH = 14-(-log10(0,1M)) = 13,00

Prima del raggiungimento del punto equivalente, è la base a essere in eccesso rispetto all’acido e la concentrazione di ioni OH– può essere calcolata in accordo con la seguente formula:

[OH^{-}] =\frac{C_{b}V_{b}-C_{a}V_{a}}{V_{a}+V_{b}}

Al raggiungimento del punto equivalente, le moli di NaOH sono state neutralizzate da un uguale numero di moli di HCl. L’uniche specie presenti sono H2O, Na+ e Cl–. Gli ioni non sono in grado di dare reazione di idrolisi salina e pertanto il pH al punto equivalente risulta uguale a 7, in virtù della reazione di autoprotolisi dell’acqua.

Aggiungendo un ulteriore quantità di acido forte, il pH si sposta verso valori più acidi. Essendo questa volta l’acido in eccesso, la concentrazione di ioni H+ può essere calcolata come:

[H^{+}] =\frac{C_{a}V_{a}-C_{b}V_{b}}{V_{a}+V_{b}}

CURVA DI TITOLAZIONE CON CALCOLI

PRIMA DEL PUNTO EQUIVALENTE

Volume titolante  
(ml)		Concentrazione ioni OH–
(mol/L)
(CbVb-CaVa)/(Va+Vb)		pH
14-(-log10[OH–])
01,00 10-113,00
58,18 10-212,91
106,67 10-212,82
155,38 10-212,73
204,29 10-212,63
253,33 10-212,52
302,50 10-212,40
351,76 10-212,25
401,11 10-212,05
455,26 10-311,72
482,04 10-311,31
48,11,94 10-311,29
48,21,83 10-311,26
48,31,73 ∙ 10-311,24
48,41,63 ∙ 10-311,21
48,51,52 ∙ 10-311,18
48,61,42 ∙ 10-311,15
48,71,32 ∙ 10-311,12
48,81,21 ∙ 10-311,08
48,91,11 ∙ 10-311,05
491,01 ∙ 10-311,00
49,19,08 ∙ 10-410,96
49,28,06∙ 10-410,91
49,37,05 ∙ 10-410,85
49,46,04 ∙ 10-410,78
49,55,03 ∙ 10-410,70
49,64,02 ∙ 10-410,60
49,73,01∙ 10-410,48
49,82,00 ∙ 10-410,30
49,91,00∙ 10-410,00
49,919,01 ∙ 10-59,95
49,928,01 ∙ 10-59,90
49,937,00∙ 10-59,85
49,946,00 ∙ 10-59,78
49,955,00 ∙ 10-59,70
49,964,00 ∙ 10-59,60
49,973,00 ∙ 10-59,48
49,982,00 ∙ 10-59,30
49,991,00 ∙ 10-59,00
49,9919,00 ∙ 10-68,95
49,9928,00∙ 10-68,90
49,9937,00 ∙ 10-68,85
49,9946,00 ∙ 10-68,78
49,9955,00 ∙ 10-68,70
49,9964,00 ∙ 10-68,60
49,9973,00 ∙ 10-68,48
49,9982,00 ∙ 10-68,30
49,9991,00 ∙ 10-68,00
49,99919,00 ∙ 10-77,95
49,99928,00 ∙ 10-77,90
49,99937,00 ∙ 10-77,85
49,99946,00 ∙ 10-77,78
49,99955,00 ∙ 10-77,70
49,99964,00 ∙ 10-77,60
49,99973,00 ∙ 10-77,48
49,99982,00 ∙ 10-77,30
49,99991,00 ∙ 10-77,00

PUNTO EQUIVALENTE

Volume titolante aggiunto: 50 ml

Concentrazione ioni H+ = 1,00 ∙ 10-7 M

pH = 7,00

DOPO IL PUNTO EQUIVALENTE

Volume titolante  (ml)Concentrazione ioni H+
(mol/L)
(CaVa-CbVb)/(Va+Vb)		pH
-log10[H+]
50,00011,00 ∙ 10-77,00
50,00022,00 ∙ 10-76,70
50,00033,00 ∙ 10-76,52
50,00044,00 ∙ 10-76,40
50,00055,00 ∙ 10-76,30
50,00066,00 ∙ 10-76,22
50,00077,00 ∙ 10-76,15
50,00088,00 ∙ 10-76,10
50,00099,00 ∙ 10-76,05
50,0011,00 ∙ 10-66,00
50,0022,00 ∙ 10-65,70
50,0033,00 ∙ 10-65,52
50,0044,00 ∙ 10-65,40
50,0055,00 ∙ 10-65,30
50,0066,00 ∙ 10-65,22
50,0077,00 ∙ 10-65,15
50,0088,00 ∙ 10-65,10
50,0099,00 ∙ 10-65,05
50,011,00 ∙ 10-55,00
50,022,00 ∙ 10-54,70
50,033,00 ∙ 10-54,52
50,044,00 ∙ 10-54,40
50,055,00 ∙ 10-54,30
50,066,00 ∙ 10-54,22
50,077,00 ∙ 10-54,16
50,087,99 ∙ 10-54,10
50,098,99 ∙ 10-54,05
50,19,99 ∙ 10-54,00
50,22,00 ∙ 10-43,70
50,32,99 ∙ 10-43,52
50,43,98 ∙ 10-43,40
50,54,98 ∙ 10-43,30
50,65,96 ∙ 10-43,22
50,76,95 ∙ 10-43,16
50,87,94 ∙ 10-43,10
50,98,92 ∙ 10-43,05
519,90 ∙ 10-43,00
521,96 ∙ 10-32,71
554,76 ∙ 10-32,32
609,09 ∙ 10-32,04
651,30 ∙ 10-31,88
701,67 ∙ 10-21,78
752,00 ∙ 10-21,70
802,31 ∙ 10-21,64
852,59 ∙ 10-21,59
902,86 ∙ 10-21,54
953,10 ∙ 10-21,51
1003,33 ∙ 10-21,48

TITOLAZIONE ACIDO FORTE CON BASE FORTE

La titolazione di un acido forte con una base forte prevede che vi sia una reazione chimica tra un acido forte e una base forte.

  • L’acido forte è l’analita, ovvero la sostanza che deve essere titolata.
  • La base forte è il titolante ovvero la sostanza che viene aggiunta all’analita.

Nella curva di titolazione viene graficato il valore del pH al variare del volume di titolante aggiunto.

La titolazione avviene fino al raggiungimento del punto equivalente, in cui la quantità di equivalenti di base eguaglia la quantità di equivalenti di acido.

Titolazione di HCl con NaOH

Si considerino 50 ml di una soluzione 0,1 M di HCl che vengono titolati con una soluzione 0,1 M di NaOH. La reazione può essere descritta come:

HCl + NaOH → H2O + Na+ + Cl–

Essendo HCl un acido forte, il pH iniziale può essere calcolato come:

pH = -log10(0,1M) = 1,00

Prima del raggiungimento del punto equivalente, è l’acido a essere in eccesso rispetto alla base e la concentrazione di ioni H+ può essere calcolata in accordo con la seguente formula:

[H^{+}] =\frac{C_{a}V_{a}-C_{b}V_{b}}{V_{a}+V_{b}}

Al raggiungimento del punto equivalente le moli di HCl sono state neutralizzate da un uguale numero di moli di NaOH. L’uniche specie presenti sono H2O, Na+ e Cl–. Gli ioni non sono in grado di dare reazione di idrolisi salina e pertanto il pH al punto equivalente risulta uguale a 7, in virtù della reazione di autoprotolisi dell’acqua.

Aggiungendo un ulteriore quantità di base forte, il pH si sposta verso valori più basici. Essendo questa volta la base in eccesso, la concentrazione di ioni OH– può essere calcolata come:

[OH^{-}] =\frac{C_{b}V_{b}-C_{a}V_{a}}{V_{a}+V_{b}}

CURVA DI TITOLAZIONE CON CALCOLI

PRIMA DEL PUNTO EQUIVALENTE

Volume titolante  
(ml)		Concentrazione ioni H+
(mol/L)
(CaVa-CbVb)/(Va+Vb)		pH
-log10[H+]
01,00 10-11,00
58,18 10-21,09
106,67 10-21,18
155,38 10-21,27
204,29 10-21,37
253,33 10-21,48
302,50 10-21,60
351,76 10-21,75
401,11 10-21,95
455,26 10-32,28
482,04 10-32,69
48,11,94 10-32,71
48,21,83 10-32,74
48,31,73 ∙ 10-32,76
48,41,63 ∙ 10-32,79
48,51,52 ∙ 10-32,82
48,61,42 ∙ 10-32,85
48,71,32 ∙ 10-32,88
48,81,21 ∙ 10-32,92
48,91,11 ∙ 10-32,95
491,01 ∙ 10-33,00
49,19,08 ∙ 10-43,04
49,28,06 ∙ 10-43,09
49,37,05 ∙ 10-43,15
49,46,04 ∙ 10-43,22
49,55,03 ∙ 10-43,30
49,64,02 ∙ 10-43,40
49,73,01 ∙ 10-43,52
49,82,00 ∙ 10-43,70
49,91,00∙ 10-44,00
49,919,01 ∙ 10-54,05
49,928,01 ∙ 10-54,10
49,937,00∙ 10-54,15
49,946,00 ∙ 10-54,22
49,955,00 ∙ 10-54,30
49,964,00 ∙ 10-54,40
49,973,00 ∙ 10-54,52
49,982,00 ∙ 10-54,70
49,991,00 ∙ 10-55,00
49,9919,00 ∙ 10-65,05
49,9928,00∙ 10-65,10
49,9937,00 ∙ 10-65,15
49,9946,00 ∙ 10-65,22
49,9955,00 ∙ 10-65,30
49,9964,00 ∙ 10-65,40
49,9973,00 ∙ 10-65,52
49,9982,00 ∙ 10-65,70
49,9991,00 ∙ 10-66,00
49,99919,00 ∙ 10-76,05
49,99928,00 ∙ 10-76,10
49,99937,00 ∙ 10-76,15
49,99946,00 ∙ 10-76,22
49,99955,00 ∙ 10-76,30
49,99964,00 ∙ 10-76,40
49,99973,00 ∙ 10-76,52
49,99982,00 ∙ 10-76,70
49,99991,00 ∙ 10-77,00

PUNTO EQUIVALENTE

Volume titolante aggiunto: 50 ml

Concentrazione ioni H+ = 1,00 ∙ 10-7 M

pH = 7,00

DOPO IL PUNTO EQUIVALENTE

Volume titolante  
(ml)		Concentrazione ioni OH–
(mol/L)
(CbVb-CaVa)/(Va+Vb)		pH
14-(-log10[H+])
50,00011,00 ∙ 10-77,00
50,00022,00 ∙ 10-77,30
50,00033,00 ∙ 10-77,48
50,00044,00 ∙ 10-77,60
50,00055,00 ∙ 10-77,70
50,00066,00 ∙ 10-77,78
50,00077,00 ∙ 10-77,85
50,00088,00 ∙ 10-77,90
50,00099,00 ∙ 10-77,95
50,0011,00 ∙ 10-68,00
50,0022,00 ∙ 10-68,30
50,0033,00 ∙ 10-68,48
50,0044,00 ∙ 10-68,60
50,0055,00 ∙ 10-68,70
50,0066,00 ∙ 10-68,78
50,0077,00 ∙ 10-68,85
50,0088,00 ∙ 10-68,90
50,0099,00 ∙ 10-68,95
50,011,00 ∙ 10-59,00
50,022,00 ∙ 10-59,30
50,033,00 ∙ 10-59,48
50,044,00 ∙ 10-59,60
50,055,00 ∙ 10-59,70
50,066,00 ∙ 10-59,78
50,077,00 ∙ 10-59,84
50,087,99 ∙ 10-59,90
50,098,99 ∙ 10-59,95
50,19,99 ∙ 10-510,00
50,22,00 ∙ 10-410,30
50,32,99 ∙ 10-410,48
50,43,98 ∙ 10-410,60
50,54,98 ∙ 10-410,70
50,65,96 ∙ 10-410,78
50,76,95 ∙ 10-410,84
50,87,94 ∙ 10-410,90
50,98,92 ∙ 10-410,95
519,90 ∙ 10-411,00
521,96 ∙ 10-311,29
554,76 ∙ 10-311,68
609,09 ∙ 10-311,96
651,30 ∙ 10-312,12
701,67 ∙ 10-212,22
752,00 ∙ 10-212,30
802,31 ∙ 10-212,36
852,59 ∙ 10-212,41
902,86 ∙ 10-212,46
953,10 ∙ 10-212,49
1003,33 ∙ 10-212,52

LEGGE DI GAY-LUSSAC

Secondo la legge di Gay-Lussac, in condizioni isocore (volume costante), la pressione di un certo quantitativo di gas ideale è proporzionale alla sua temperatura assoluta.

P = kT

  • P = pressione
  • T = temperatura espressa in gradi Kelvin (K)
  • k = costante di proporzionalità

S’immagini di avere delle molecole di gas all’interno di un contenitore a pareti rigide come uno spray all’interno di una bomboletta. Da un punto di vista microscopico, la pressione all’interno del contenitore è legata al numero di urti che le molecole esercitano contro le pareti del contenitore. Aumentando la temperatura, le molecole iniziano a muoversi più vorticosamente con un conseguente incremento del numero di urti (Figura 1).

Figura 1 – Aumento della pressione al crescere della temperatura in condizioni isocore

Graficando la pressione in funzione della temperatura espressa in gradi Kelvin, si ottiene una retta la cui pendenza è pari a P0/273,15 dove con P0 s’intende la pressione alla temperatura di 0°C.

CONCETTI CHIAVE:

  • La legge di Gay-Lussac afferma la proporzionalità diretta che vi è per una certa quantità di gas tra la temperatura assoluta e la sua pressione in condizioni isocore.
  • La legge di Gay-Lussac si applica a tutti i gas il cui comportamento viene assunto come ideale.
  • La legge di Gay-Lussac rappresenta uno dei capisaldi per la formulazione dell’equazione di stato dei gas ideali.

GAS REALI

Il comportamento di un gas reale è approssimabile a quello di un gas ideale in certi intervalli di pressione e temperatura, mentre in altre condizioni può discostarsi anche in maniera significativa.

Le maggiori deviazioni dal comportamento ideale sono dovute a due fattori:

  • Il volume occupato da una singola particella gassosa.
  • La presenza di interazioni tra le particelle.

Il fattore di compressibilità

Per un gas ideale il rapporto PV/nRT = 1 per ogni valore di pressione e temperatura.

Per un gas reale si introduce una nuova grandezza chiamata fattore di compressibilità Z:

Z =\frac{PV}{nRT}

Tanto più il comportamento del gas reale si avvicina quello ideale, tanto più il valore di Z tende a 1.

A valori più bassi di pressione, il valore di Z può scendere al di sotto di 1. Questo può essere spiegato considerando un gas reale più comprimibile di un gas ideale in virtù delle forze di attrazione tra le particelle che facilitano il loro avvicinamento.

A parità di pressione esercitata, il recipiente contenente un gas reale viene ridotto a un volume minore rispetto a quello contenente un gas ideale.

\frac{P\cdot V_{reale}}{nRT}<\frac{P\cdot V_{ideale}}{nRT}

A più alti valori di pressione inizia a farsi sentire l’effetto del volume occupato dalle singole particelle che rende più difficoltosa la compressione. A parità di pressione esercitata, è questa volta il recipiente contenente il gas ideale a essere ridotto a un volume minore rispetto a quello contenente un gas reale.

\frac{P\cdot V_{reale}}{nRT}>\frac{P\cdot V_{ideale}}{nRT}

Al crescere della temperatura vi è un incremento dell’energia cinetica posseduta dalle particelle le quali acquistano anche una maggiore mobilità. Questi effetti rendono meno consistente l’attrazione tra le particelle così come tendono ad aumentare la loro distanza vanificando l’effetto del volume proprio di ciascuna di essa. Aumentando la temperatura, il comportamento di un gas reale è approssimabile a quello di un gas ideale.

EQUAZIONE DI VAN DER WAALS

Johannes Van Der Waals propose una correzione all’equazione di stato dei gas ideali, tenendo conto dell’effetto del volume occupato da una singola particella e delle interazioni di natura attrattiva presenti.

L’equazione di Van Der Walls può essere scritta come:

(P+\frac{an^{2}}{V^{2}})(V-nb)=nRT

CORREZIONE DEL VOLUME

Il termine volume può essere corretto tenendo conto che le particelle gassose non sono puntiformi ma occupano uno spazio (covolume) che non è accessibile a un’altra particella.

V = Videale – nb

  • n = numero di moli di gas
  • b = costante legata alle dimensioni delle particelle

CORREZIONE DELLA PRESSIONE

Quando una molecola urta contro la parete del recipiente, la forza d’impatto viene attenuata dall’attrazione esercitata delle altre particelle al centro. Questo effetto è tanto più marcato quanto maggiore è la densità di particelle nel recipiente e quanto maggiore è l’effetto intrinseco d’interazione.

Preale < Pideale

Nell’equazione di stato dei gas ideali occorre introdurre un termine correttivo che aggiunga alla pressione misurata un termine proporzionale al livello d’interazione tra le particelle e al quadrato della densità tra le particelle.

P_{ideale}= P_{reale} + \frac{an^{2}}{V^{2}}

  • n = numero di moli
  • a = termine che tiene conto dell’effetto intrinseco delle interazioni tra le particelle

Le molecole che interagiscono tra loro più fortemente sono quelle che risentono maggiormente della deviazione dal comportamento ideale. Un esempio è rappresentato dall’ammoniaca le cui molecole interagiscono tra loro più fortemente rispetto alle molecole di idrogeno e azoto in virtù dei legami a idrogeno.

CONCETTI CHIAVE:

  • I gas reali hanno un comportamento che si discosta da quello ideale.
  • A più basse pressioni l’effetto delle attrazioni rende un gas reale più comprimibile di uno ideale.
  • A più alte pressioni l’effetto del covolume rende un gas reale meno comprimibile di uno ideale.
  • L’equazione di Van Der Waals corregge l’equazione di stato dei gas ideali tenendo conto di questi effetti.

pH e pOH

pH

Il pH si ottiene calcolando l’opposto del logaritmo decimale dalla concentrazione di ioni H+.

pH = -log10 [H+]

Se la concentrazione degli ioni H+ è uguale a 10-1 M allora il valore di pH risulta pari a 1.

Se la concentrazione degli ioni H+ è uguale a 10-10 M allora il valore di pH risulta pari a 10.

Se la concentrazione degli ioni H+ è uguale a 10-7 M allora il valore di pH risulta pari a 7.

All’aumentare della concentrazione di ioni H+ corrisponde un abbassamento del valore del pH.

Una soluzione può definirsi:

  • Acida se pH<7
  • Neutra se pH=7
  • Basica se pH>7

Il pH viene misurato in una scala che va da 0 a 14 che corrisponde a concentrazioni di ioni H+ che vanno da 1M a 10-14M. Sebbene siano rari, possono esistere valori di pH negativi per soluzioni in cui la concentrazione di ioni H+ è superiore a 1M e valori di pH superiori a 14, per soluzioni in cui la concentrazione di ioni H+ è inferiore a 10-14M.

pOH

Il pOH si ottiene calcolando l’opposto del logaritmo decimale dalla concentrazione di ioni OH–.

pOH = -log10 [OH–]

Se la concentrazione degli ioni OH– è uguale a 10-1 M allora il valore di pOH risulta pari a 1.

Se la concentrazione degli ioni OH– è uguale a 10-10 M allora il valore di pOH risulta pari a 10.

Se la concentrazione degli ioni OH– è uguale a 10-7 M allora il valore di pOH risulta pari a 7.

All’aumentare della concentrazione di ioni OH– corrisponde un abbassamento del valore del pOH.

Una soluzione può definirsi:

  • Acida se pOH >7
  • Neutra se pOH=7
  • Basica se pOH < 7

Il pOH viene misurato in una scala che va da 0 a 14 che corrisponde a concentrazioni di ioni OH– che vanno da 1M a 10-14M. Sebbene siano rari, possono esistere valori di pOH negativi per soluzioni in cui la concentrazione di ioni OH– è superiore a 1M e valori di pOH superiori a 14, per soluzioni in cui la concentrazione di ioni OH– è inferiore a 10-14M.

Relazione tra pH e pOH

Si può individuare una relazione tra pH e pOH secondo cui:

pH + pOH = 14

Se volessimo tradurre questa relazione in termini di concentrazioni si può scrivere:

[H+]·[OH–] = 10-14

CONCETTI CHIAVE

  • Il pH misura la concentrazione di ioni H+ in soluzione e può essere calcolato come pH = -log10[H+].
  • Il pOH misura la concentrazione di ioni OH– in soluzione e può essere calcolato come pOH = -log10[OH–].
  • La relazione tra pH e pOH è pH + pOH = 14.

COSTANTE DI DISSOCIAZIONE BASICA

La costante di dissociazione basica Kb è una costante d’equilibrio utilizzata per descrivere la reazione di una base in acqua. Tanto più elevato è il valore di Kb tanto maggiore è la forza della base.

Si prenda la seguente reazione di idrolisi basica:

NH3 + H2O ⇄ NH4++ OH–

La costante di dissociazione basica può essere scritta come:

K_{b}= \frac{[NH_{4}^{+}][OH^{-}]}{[NH_{3}]}

Valori elevati di Kb indicano che al raggiungimento dell’equilibrio chimico, i prodotti sono presenti in maggiore quantità rispetto ai reagenti. Questo è il comportamento tipico delle basi forti.

Bassi valori di Kb indicano il prevalere della concentrazione dei reagenti rispetto ai prodotti una volta raggiunte le condizioni di equilibrio chimico. Questo è il comportamento tipico delle basi deboli.

Un ulteriore modo per descrivere la costante di dissociazione basica è quello di utilizzare la pKb di una base. Analogamente a quanto visto per il pH, il termine pKb indica:

pKb = -log10Kb

Basi poliprotiche

Le basi poliprotiche sono basi in grado di accettare più di uno ione H+. A ogni reazione è associata una specifica costante di dissociazione basica Kb.

PO43- + H2O ⇄ HPO42- + OH– Kb1 = 2,40 · 10-2

HPO42- + H2O ⇄ H2PO4– + OH– Kb2 = 1,60 · 10-7

H2PO4– + H2O ⇄ H3PO4 + OH– Kb3 = 1,40 · 10-12

Relazione tra costante di dissociazione acida e basica

Per ogni reazione di idrolisi basica è possibile scrivere la reazione di idrolisi acida dell’acido coniugato:

Idrolisi basica: NH3 + H2O ⇄ NH4++ OH– Kb = 1,79 · 10-5

Idrolisi acida: NH4+ + H2O ⇄ H3O+ + NH3 Ka = 5,59 · 10-10

Esiste una relazione tra Ka e Kb secondo cui:

Ka · Kb = Kw

Kw = 1,00 · 10-14

CONCETTI CHIAVE:

  • La costante di dissociazione basica Kb misura la forza di una base.
  • Alti valori di Kb appartengono a basi che si reagiscono fortemente in acqua.
  • Bassi valori di Kb appartengono a basi che si reagiscono debolmente in acqua.
  • Le basi poliprotiche sono in grado di accettare più di uno ione H+.
  • La relazione tra Ka e Kb è la seguente: Ka · Kb = Kw

COSTANTE DI DISSOCIAZIONE ACIDA

La costante di dissociazione acida Ka è una costante d’equilibrio utilizzata per descrivere la reazione di dissociazione di un acido. Tanto più elevato è il valore di Ka tanto maggiore è la forza dell’acido.

Si prenda la seguente reazione:

CH3COOH + H2O ⇄ CH3COO–+ H3O+

La costante di dissociazione acida può essere scritta come:

K_{a}= \frac{[H_{3}O^{+}][CH_{3}COO^{-}]}{[CH_{3}COOH]}

Valori elevati di Ka indicano che al raggiungimento dell’equilibrio chimico, la forma dissociata dell’acido (numeratore), prevale sulla forma indissociata (denominatore). Questo è il comportamento tipico degli acidi forti.

Bassi valori di Ka indicano il prevalere della forma indissociata dell’acido rispetto alla forma dissociata una volta raggiunte le condizioni di equilibrio chimico. Questo è il comportamento tipico degli acidi deboli.

Un ulteriore modo per descrivere la costante di dissociazione acida è quello di utilizzare la pKa di un acido. Analogamente a quanto visto per il pH, il termine pKa indica:

pKa = -log10Ka

Acidi poliprotici

Gli acidi poliprotici sono acidi in grado di donare più di uno ione H+. A ogni dissociazione è associata una specifica costante di dissociazione. All’aumentare del numero di dissociazioni la Ka assume un valore minore.

H3AsO4 + H2O ⇄ H3O+ + H2AsO4– I Dissociazione Ka1 = 6,46 · 10-3

H2AsO4– + H2O ⇄ H3O+ + HAsO42- II Dissociazione Ka2 = 1,15 · 10-7

HAsO42- + H2O ⇄ H3O+ + AsO43- III Dissociazione Ka3 = 3,16 · 10-12

Relazione tra costante di dissociazione acida e basica

Per ogni reazione di dissociazione acida è possibile scrivere la reazione di idrolisi basica della base coniugata dell’acido:

Dissociazione acida: CH3COOH + H2O ⇄ CH3COO–+ H3O+ Ka = 1,75 · 10-5

Idrolisi basica: CH3COO– + H2O ⇄ CH3COOH+ OH– Kb = 5,71 · 10-10

Esiste una relazione tra Ka e Kb secondo cui:

Ka · Kb = Kw

Kw = 1,00 · 10-14

CONCETTI CHIAVE:

  • La costante di dissociazione acida Ka misura la forza di un acido.
  • Alti valori di Ka appartengono ad acidi che si dissociano fortemente in acqua.
  • Bassi valori di Ka appartengono ad acidi che si dissociano debolmente in acqua.
  • Gli acidi poliprotici sono in grado di donare più di uno ione H+.
  • La relazione tra Ka e Kb è la seguente: Ka · Kb = Kw

IDRACIDI

Gli idracidi sono composti binari che hanno formula HX:

  • H è l’atomo di idrogeno che compare sempre come primo nella formula.
  • X può essere uno dei seguenti non metalli: fluoro, cloro, bromo, iodio, astato, zolfo, selenio, tellurio, azoto e gruppo cianidrico.

Nella formula degli idracidi, l’idrogeno ha sempre numero d’ossidazione +1, mentre il non metallo ha numero d’ossidazione negativo.

NOMENCLATURA IDRACIDI

NOMENCLATURA IUPAC

La nomenclatura IUPAC prevede di nominare i composti seguendo la regola dell’incrocio, partendo dal composto che compare come secondo e poi citando quello che compare come primo. All’elemento che compare come secondo viene aggiunto il suffisso uro.

Prima di ogni elemento viene indicato un prefisso che identifica in maniera inequivocabile il numero di atomi presenti.

HF – Fluoruro di idrogeno

HCl – Cloruro di idrogeno

HBr – Bromuro di idrogeno

HI – Ioduro di idrogeno

HAt – Astaturo di idrogeno

H2S – Solfuro di diidrogeno

H2Se – Seleniuro di diidrogeno

H2Te – Tellururo di diidrogeno

HN3 – Triazoturo di idrogeno

HCN – Cianuro di idrogeno

NOMENCLATURA TRADIZIONALE

La nomenclatura tradizionale non prevede l’utilizzo di prefissi. La nomenclatura viene costruita seguendo il seguente schema:

ACIDO + NOME DEL NON METALLO + IDRICO

HF – Acido fluoridrico

HCl – Acido cloridrico

HBr – Acido bromidrico

HI – Acido iodidrico

HAt – Acido astatidrico

H2S – Acido solfidrico

H2Se – Acido selenidrico

H2Te – Acido telluridrico

HN3 – Acido azotidrico

HCN – Acido cianidrico

CONCETTI CHIAVE:

  • Gli idracidi hanno formula HX (idrogeno + non metallo).
  • L’idrogeno, che compare sempre come primo, ha numero d’ossidazione +1.
  • Il non metallo, che compare sempre come secondo, ha numero d’ossidazione negativo.
  • La nomenclatura tradizionale prevede l’utilizzo dello schema: ACIDO + NOME DEL NON METALLO + IDRICO.

ESERCIZIO SVOLTO 1:

Nominare il seguente composto seguendo le regole della nomenclatura IUPAC, tradizionale e notazione di Stock:

CoH3

La nomenclatura IUPAC prevede di nominare prima l’idrogeno e poi il cobalto (regola dell’incrocio) ciascun preceduto dal prefisso che ne identifica il numero di atomi.

CoH3 – Triidruro di cobalto

La nomenclatura tradizionale prevede di nominare prima l’idrogeno e poi il cobalto (regola dell’incrocio) senza alcun prefisso che ne identifichi il numero di atomi. In presenza di più numeri d’ossidazione del metallo, quello più basso è accompagnato dal suffisso oso, mentre quello più alto dal suffisso ico.

Nel composto CoH3 il cobalto ha numero d’ossidazione +3. Guardando la tavola periodica, si osserva come il cobalto abbia numeri d’ossidazione +2 e +3. Pertanto, il suffisso da attribuire al metallo in questo caso è ico.

CoH3 – Ossido cobaltico

La notazione di Stock prevede nel formulare il nome, l’utilizzo del seguente schema:

IDRURO di METALLO (stato d’ossidazione del metallo in numero romano)

CoH3 – Idruro di cobalto (III)

ESERCIZIO SVOLTO 2:

Determinare la formula del seguente composto:

IDRURO PIOMBOSO

Il composto rientra nella categoria degli idruri metallici. Guardando la tavola periodica, si evidenzia come il piombo appartenga al gruppo IVA e abbia come numeri di ossidazione +2 e +4, mentre l’idrogeno abbia numero d’ossidazione -1. Il suffisso oso indica che il metallo ha il numero d’ossidazione positivo più basso, ovvero +2.

Essendo il composto nel complesso neutro esso deve essere costituito da due atomi di idrogeno e uno di piombo:

PbH2