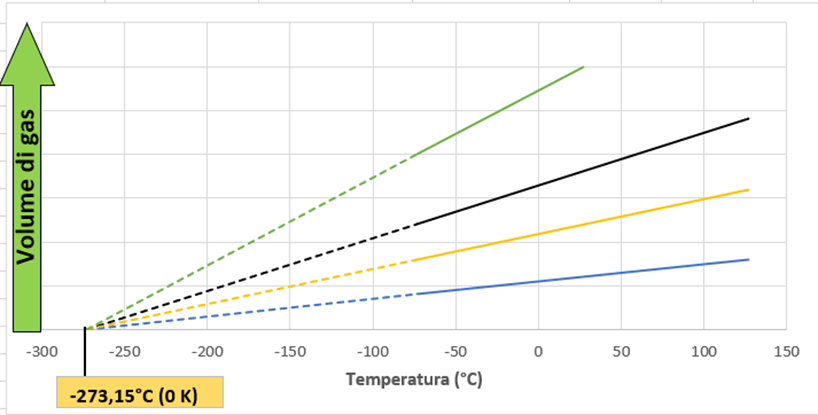
Secondo la legge di Gay-Lussac, in condizioni isocore (volume costante), la pressione di un certo quantitativo di gas ideale è proporzionale alla sua temperatura assoluta.
P = kT
- P = pressione
- T = temperatura espressa in gradi Kelvin (K)
- k = costante di proporzionalità
S’immagini di avere delle molecole di gas all’interno di un contenitore a pareti rigide come uno spray all’interno di una bomboletta. Da un punto di vista microscopico, la pressione all’interno del contenitore è legata al numero di urti che le molecole esercitano contro le pareti del contenitore. Aumentando la temperatura, le molecole iniziano a muoversi più vorticosamente con un conseguente incremento del numero di urti (Figura 1).
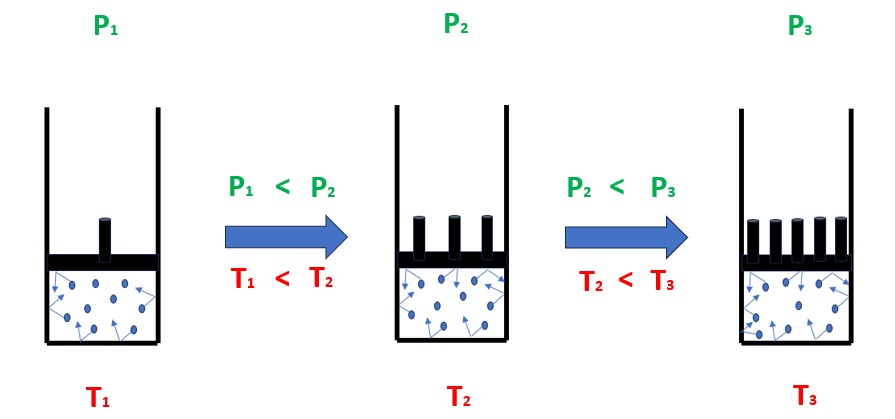
Figura 1 – Aumento della pressione al crescere della temperatura in condizioni isocore
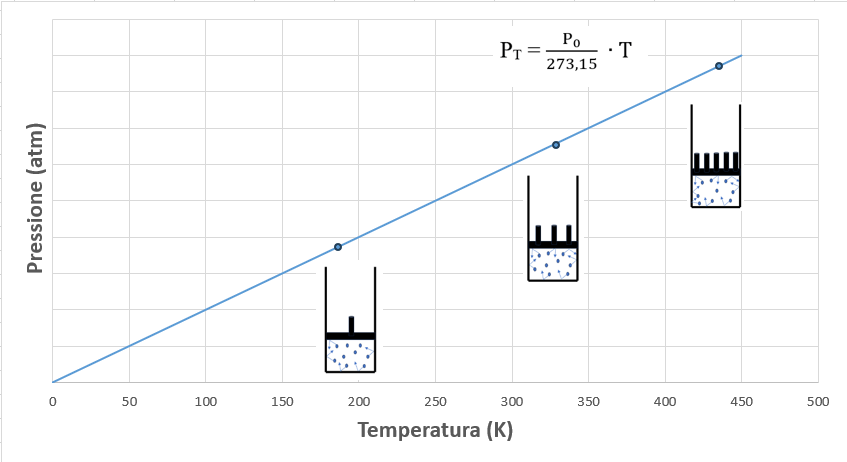
Graficando la pressione in funzione della temperatura espressa in gradi Kelvin, si ottiene una retta la cui pendenza è pari a P0/273,15 dove con P0 s’intende la pressione alla temperatura di 0°C.
CONCETTI CHIAVE:
- La legge di Gay-Lussac afferma la proporzionalità diretta che vi è per una certa quantità di gas tra la temperatura assoluta e la sua pressione in condizioni isocore.
- La legge di Gay-Lussac si applica a tutti i gas il cui comportamento viene assunto come ideale.
- La legge di Gay-Lussac rappresenta uno dei capisaldi per la formulazione dell’equazione di stato dei gas ideali.